背景
最近在和同事探讨一个技术问题,他们现在遇到一个场景手上会有几百个门店点坐标信息,需要在拿到用户的坐标之后计算出离用户最近的几家门店并计算他们之间的距离。
思考
我的第一想法很简单,找附近的,坐标系不就经纬度、横纵坐标吗?那不就是横坐标差值和纵坐标差值最小的么?勾股定理,也就是欧几里得距离,两个坐标差再平方和开根号。
具体来说就是帮所有的门店的横纵坐标建个索引,可以用二叉树什么的,然后根据横纵坐标按照索引找应该来说很快就能找到,感觉是很简单的问题。
质疑
领导提醒我,计算两个坐标之间的距离怎么可以用勾股定理? 有你想的这么简单么?
是的! 我们的世界是一个球体,我们的地图之所以横纵等比例是为了方便我们来看,宏观来说,我们的地图比例需要考虑高低纬度的问题,计算距离的时候还要考虑球体表面弧度的问题。
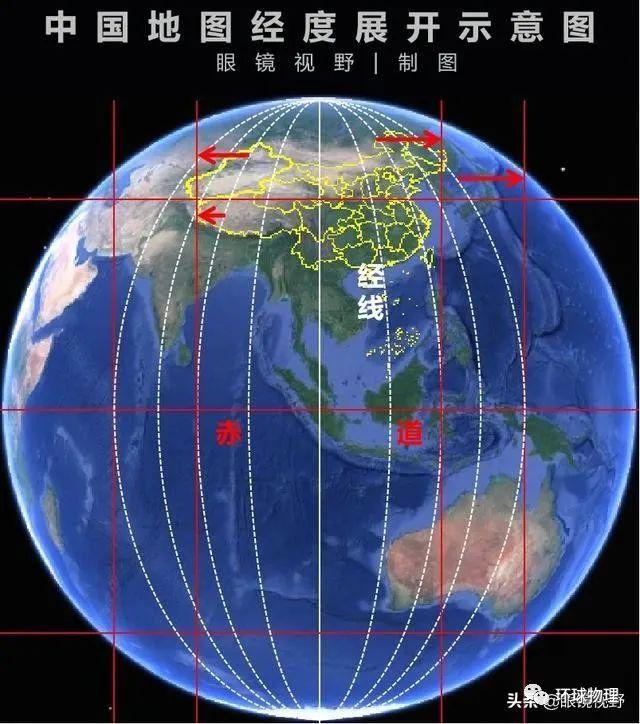
如果简单的使用勾股定理的话,在赤道附近,两点距离不是很远的情况下,可能误差小一点,如果靠近南北极或者两个点的距离很远,使用这种方式计算,可能会有很大的误差。
查了资料,计算地球上两点距离应该使用合适的距离计算公式,比如哈弗辛公式(Haversine formula),来计算两点间的距离。这个公式考虑了地球的曲率,适用于经纬度坐标。
哈弗辛距离(Haversine distance)是地球上两点之间的最短距离,通常用于计算航空和航海中的距离。在Python中,可通过使用math库中的sin、cos、radians和sqrt等函数来计算哈弗辛距离。具体实现如下:
#!/usr/bin/python
# -*- coding: UTF-8 -*-
import math
# 计算两点之间的哈弗辛距离
def haversine(lon1, lat1, lon2, lat2):
# 将十进制度数转化为弧度数
lon1, lat1, lon2, lat2 = map(math.radians, [lon1, lat1, lon2, lat2])
# Haversine公式
dlon = lon2 - lon1
dlat = lat2 - lat1
a = math.sin(dlat / 2) ** 2 + math.cos(lat1) * math.cos(lat2) * math.sin(dlon / 2) ** 2
c = 2 * math.asin(math.sqrt(a))
r = 6371 # 地球平均半径,单位为公里
return c * r
# 计算一组坐标中的最小哈弗辛距离
def min_haversine_distance(coords):
min_dist = float("inf")
n = len(coords)
for i in range(n):
for j in range(i+1, n):
lon1, lat1 = coords[i]
lon2, lat2 = coords[j]
dist = haversine(lon1, lat1, lon2, lat2)
if dist < min_dist:
min_dist = dist
return min_dist
# 示例
coords = [(116.3975, 39.9086), (121.4737, 31.2304), (113.2644, 23.1291)]
min_dist = min_haversine_distance(coords)
print(min_dist)
但是如果我们使用这个公式的话,似乎给既定门店建立坐标索引配合公式计算是件较为复杂的事情。
我的方案
先来评估性能
#!/usr/bin/python
# -*- coding: UTF-8 -*-
import time
import random
import math
def haversine(coord1, coord2):
"""
计算两个经纬度点之间的哈弗辛距离。
coord1 : (lat, lon) 第一个点的坐标
coord2 : (lat, lon) 第二个点的坐标
"""
R = 6371 # 地球半径,单位为公里
lat1, lon1 = coord1
lat2, lon2 = coord2
dlat = math.radians(lat2 - lat1)
dlon = math.radians(lon2 - lon1)
a = math.sin(dlat / 2)**2 + math.cos(math.radians(lat1)) * math.cos(math.radians(lat2)) * math.sin(dlon / 2)**2
c = 2 * math.atan2(math.sqrt(a), math.sqrt(1 - a))
return R * c
# 生成500个随机坐标(经纬度范围:-90至90纬度,-180至180经度)
random_coords = [(random.uniform(-90, 90), random.uniform(-180, 180)) for _ in range(500)]
# 生成一个随机目标坐标点
target_coord = (random.uniform(-90, 90), random.uniform(-180, 180))
# 记录开始时间
start_time = time.time()
# 对每个坐标使用哈弗辛公式计算与目标点的距离,并找出最近的三个坐标
distances = [haversine(coord, target_coord) for coord in random_coords]
nearest_three = sorted(enumerate(distances), key=lambda x: x[1])[:3]
# 记录结束时间
end_time = time.time()
# 计算总执行时间
execution_time = end_time - start_time
print(nearest_three, execution_time)
# 结果 500门店:[(132, 555.3770645723912), (21, 555.5494623132214), (419, 667.7649961673167)] 0.0007128715515136719
# 结果 5000门店: [(2491, 108.14873420218066), (3789, 253.1841479656292), (928, 282.3962010223639)] 0.006649494171142578
我跑了些测试,如果按照500个门店来算,硬跑哈弗辛公式来计算,500个门店的话不到1毫秒可以出结果。如果扩展到5000个门店7毫秒左右也能出结果。
也就是说如果门店数量可控,硬跑算法遍历所有门店似乎是可行的。但是如果门店数量更多,比如100万 1000万个门店,似乎这个算法耗时应该也会按照数量级增长。
我觉得可行的方案是先按照勾股定理的方式初筛 ,筛完之后再用哈弗辛公式精确的去泡,可能是更优的方式。
以下是使用KD树来构建门店坐标数据库,然后使用欧几里得距离来找最近的门店:
#!/usr/bin/python
# -*- coding: UTF-8 -*-
import random
import time
class Node:
""" A class representing a node in the KDTree. """
def __init__(self, point, left=None, right=None):
self.point = point
self.left = left
self.right = right
def build_kdtree(points, depth=0):
""" Builds a KDTree from the given list of points. """
if not points:
return None
# Select axis based on depth so that axis cycles through all valid values
k = len(points[0]) # Assumes all points have the same dimension
axis = depth % k
# Sort point list and choose median as pivot element
points.sort(key=lambda x: x[axis])
median = len(points) // 2
# Create node and construct subtrees
return Node(
point=points[median],
left=build_kdtree(points[:median], depth + 1),
right=build_kdtree(points[median + 1:], depth + 1)
)
def squared_distance(point1, point2):
""" Calculates the squared Euclidean distance between two points. """
return sum((p1 - p2) ** 2 for p1, p2 in zip(point1, point2))
def closest_point_kdtree(root, target, depth=0):
""" Finds the closest point in the KDTree to the target point. """
if root is None:
return float('inf'), None
k = len(target)
axis = depth % k
next_branch = None
opposite_branch = None
# Choose the next branch to search
if target[axis] < root.point[axis]:
next_branch = root.left
opposite_branch = root.right
else:
next_branch = root.right
opposite_branch = root.left
# Search next branch
best_dist, best_point = closest_point_kdtree(next_branch, target, depth + 1)
# Update best point and distance if necessary
current_dist = squared_distance(target, root.point)
if current_dist < best_dist:
best_dist = current_dist
best_point = root.point
# Check if we need to search the opposite branch
if (target[axis] - root.point[axis]) ** 2 < best_dist:
dist, point = closest_point_kdtree(opposite_branch, target, depth + 1)
if dist < best_dist:
best_dist = dist
best_point = point
return best_dist, best_point
# Example usage
example_points = [(7, 2), (5, 4), (9, 6), (2, 3), (4, 7), (8, 1)]
tree = build_kdtree(example_points)
closest_distance, closest_point = closest_point_kdtree(tree, (6, 6))
closest_point
def generate_random_points(num_points, range_limit=1000):
""" Generate a list of random points within the given range. """
return [(random.uniform(-range_limit, range_limit), random.uniform(-range_limit, range_limit)) for _ in range(num_points)]
def test_kdtree_performance(points, kdtree, num_tests=100):
""" Test the performance of the KDTree-based nearest neighbor algorithm. """
total_time = 0
for _ in range(num_tests):
# Select a random target point
target = random.choice(points)
# Measure the time taken to find the closest point
start_time = time.time()
closest_point_kdtree(kdtree, target)
end_time = time.time()
total_time += (end_time - start_time)
# Calculate the average time per query
average_time = total_time / num_tests
return average_time
# 随机生成1000万个坐标
num_points = 10_000_000
random_points = generate_random_points(num_points)
# 构建 KDTree
start_time = time.time()
kdtree = build_kdtree(random_points)
end_build_time = time.time()
print(f"Time to build KDTree: {end_build_time - start_time} seconds")
# Test the KDTree performance
average_query_time = test_kdtree_performance(random_points, kdtree)
print(f"Average query time: {average_query_time} seconds")
我们发现即使是千万级别数据量也是微妙级别的查询时间,所以我们可以使用这个方式初筛出1000个最近的门店,然后再使用前面的方式精确的找出最近的3个店,并计算出他们的距离。
参考资料:
https://zhuanlan.zhihu.com/p/23966698
https://k.sina.cn/article_6367168142_17b83468e019013zlv.html